Comprehensive Guide on Sigmoid Function
Start your free 7-days trial now!
What is the sigmoid function?
The sigmoid function, often denoted as $\sigma(x)$, is defined as follows:
The sigmoid function is named as such because it is S-shaped, as can be seen from its graph:
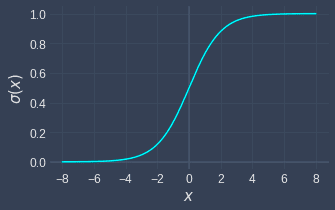
Note the following:
the domain of the sigmoid function is unbounded from $-\infty$ to $\infty$.
the range is bounded between $0$ and $1$; the output can become extremely close to $0$ or $1$, but it will never reach the boundaries.
Derivative of Sigmoid Function
The beauty of the sigmoid function is that its derivative is extremely clean:
This is a very useful property because we often encounter situations in machine learning where we need to compute the derivative of the sigmoid function. For instance, the update rule for gradient descent in logistic regression requires this derivative.
The proof does not require any advanced calculus:
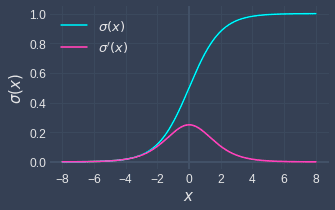
Graph of Sigmoid function and its derivative
Here's a graph of the sigmoid function and its derivative:
Implementation using Python
Here's the sigmoid function as well as its derivative implemented in Python using NumPy:







