account_circle
Profile
exit_to_app
Sign out
search
keyboard_voice
close
Searching Tips
Search for a recipe:
"Creating a table in MySQL"
"Creating a table in MySQL"
Search for an API documentation: "@append"
Search for code: "!dataframe"
Apply a tag filter: "#python"
Useful Shortcuts
/ to open search panel
Esc to close search panel
↑↓ to navigate between search results
⌘d to clear all current filters
⌘Enter to expand content preview
Doc Search
Code Search Beta
SORRY NOTHING FOUND!
mic
Start speaking...
Voice search is only supported in Safari and Chrome.
Master the Math for Data Science
Get access to 100+ comprehensive guides for $4.9 per month
Start my 7-days free trial
(no card required)
(no card required)
Linear algebra
Prob and stats
Machine learning
1. Vectors
Introduction
Position vectors
Planes
Dot product
2. Matrices
Introduction
Transpose of matrices
Trace of matrices
Invertible matrices
Elementary matrices
3. Linear equations
System of linear equations
Gaussian Elimination
Pivot positions and columns
Linear dependence and independence
Linear transformation
4. Matrix determinant
Introduction
Determinant of elementary matrices
Invertibility, multiplicative and transpose properties of determinants
Laplace expansion theorem
Cramer's rule and finding inverse matrix using determinants
Geometric interpretation
5. Vector space
Subspace
Relationship between pivots and linear dependence
Spanning Set of a vector space
Basis vectors
Constructing a basis for a vector space
Null space
Column space
Rank and nullity
6. Special matrices
Symmetric matrices
Triangular matrices
Diagonal matrices
Block matrices
LU factorization
7. Eigenvalues and Eigenvectors
Introduction
Basic properties
Eigenspace and eigenbasis
Similar matrices
Diagonalization
Algebraic and geometric multiplicity
8. Orthogonality
Orthogonal projections
Orthonormal sets and bases
Orthogonal complement
Orthogonal matrices
Least squares
Gram-Schmidt process
9. Matrix decomposition
QR decomposition
Orthogonal diagonalization
Positive definite matrices
Schur's triangulation theorem
Cholesky decomposition
Singular value decomposition
Data compression using singular value decomposition
1. Basics of statistics
Population, samples and sampling techniques
Measures of central tendency
Measures of spread
Quantiles, quartiles and percentiles
Histogram
Box-plot diagrams
2. Basics of probability theory
Basics of set theory and Venn diagrams
Counting with permutations
Counting with combinations
Sample space, events and probability axioms
Conditional probability
Multiplication and addition rule
Law of total probability
Bayes' theorem
3. Random variables
Random variables
Expected value
Properties of expected value
Variance
Properties of variance
Covariance
Correlation
4. Point estimation
Sample estimators
Sample mean
Sample variance
Sample covariance
Sample correlation
Unbiased estimator
Mean squared error
Sampling distribution of the sample mean
5. Discrete probability distributions
Probability mass function
Binomial distribution
Geometric distribution
Negative binomial distribution
Hypergeometric distribution
Poisson distribution
1. ML models
Simple linear regression
Logistic regression
k-means clustering
Hierarchical clustering
DBSCAN
Naive bayes
Decision trees
k-nearest neighbors
Perceptrons
2. Feature engineering
Feature scaling
Log transformation
Text vectorization
Grid search
Random search
Principal component analysis
3. Optimization
Gradient descent
4. Model evaluation
Confusion matrix
ROC curve
Cross validation
Mean squared error
Mean absolute error
Root mean squared error
r-squared
We're not just another math course
Most DS courses either:
- gloss over the technical details, or
- throw complex math equations without explanation
We achieve the best of worlds by deep-diving into the technical details while developing your intuition with:
format_list_numberedstep-by-step proofs
diagrams
simple examples
Theorem.
Product of block matrices (3)
Suppose we have two block matrices where each matrix is composed of four sub-matrices. The product of the two block matrices is:
Note that the shape of the matrices must match for the matrix product to be valid. For instance, the number of columns of
We're not just another math course
Most DS courses either gloss over the details or throw around complex math equations without explanation. We achieve the best of both worlds by deep-diving into the technical details while developing your intuition with:
format_list_numbered
Step-by-step proofs
local_library
Insightful diagrams
layers
Simple examples
Elevate your learning experience
priorityRigorous content
We dive deeper into the technical details than any other online course.
boltEvery theorem is proven
We offer an intuitive step-by-step proof for every theorem - no exceptions!
mediationBeginner-friendly
We go from basic high school to advanced undergraduate mathematics.
boltBlazing-fast search
Find definitions, theorems and topics using our search engine without navigating to a new page!
mapInteractive map
Visualize the connections between the math topics. Track your learning progress and complete the map!
helpAsk questions
Need help understanding the content? Ask us questions and clarify your doubts!
Your personalized learning path
Save time by learning only the relevant topics based on your goals
Instant content preview
Hover over a link to instantly see a preview of the page - no need to open up a new tab!
Instant search
Find definitions, theorems and topics using our search engine without navigating to a new page!
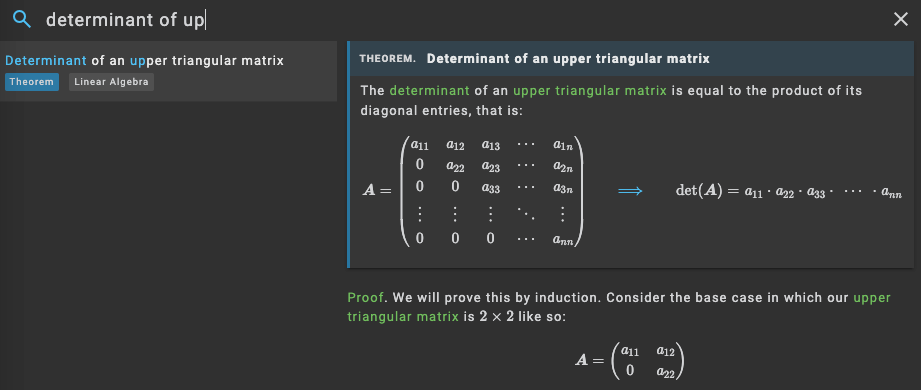
Side-by-side references
Show linked definitions, theorems and examples on the left side panel for reference!
Meet the team
Obtained a bachelors at UTokyo, a masters of DS at HKU, and now working as a MLE. I'm mainly in charge of the tech-side of SkyTowner, and I love writing articles about data science!
Graduated from UTokyo, and now working in the finance industry. I consider myself a citizen developer and write about topics as they come!
Eva
Graduated from HKUST, and now brushing up my programming skills. I enjoy documenting my learning process on SkyTowner!
Ready to deep dive into data science?
done100+ comprehensive guides on linear algebra, statistics and ML
doneDashboard to track learning progress
doneInteractive map with progress tracker
doneReal-time search for all definitions, theorems and articles
doneSide-by-side references to definitions and theorems
doneLive-preview of content on hover
doneAsk questions when stuck
doneEvery article loads in <500ms
doneNo ads
Start my 7-days free trial
(no card required)
FAQ
Why should I pay if other resources are free?
We emphasize on the quality of your education - you'll learn much faster and deeper with our guides than you would by reading through some blog post.
I'm not good at math. Is SkyTowner right for me?
Our guides are beginner-friendly and we have lots of diagrams and examples to help you grasp abstract concepts! Also, we'll do our best to help if you get stuck!
