Introduction to vectors in linear algebra
Start your free 7-days trial now!
Vectors
A vector is an object with both a magnitude (length) and a direction. An object with only the magnitude is called a scalar (e.g. $5$, $\pi$).
Vectors can be represented using an arrow that connects two points. For instance, consider the following two points:
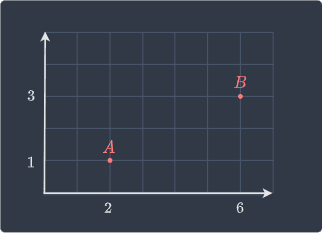
The vector $\overrightarrow{AB}$ that points from $A$ to $B$ is as follows:
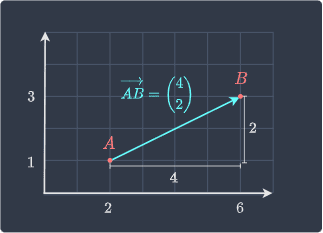
In two-dimensional space, the vector $\overrightarrow{AB}$ contains two numbers:
the first (top) component of the vector represents the horizontal distance between the points. This is also called the horizontal or $x$ component.
the second (bottom) component of the vector represents the vertical distance between the two points. This is also called the vertical or $y$ component.
Note the following two terms:
the start point of the vector is called the tail - $A$ is the tail in this case.
the end point of the vector is called the head - $B$ is the head in this case.
Vectors are typically represented using a lowercase bold letter (e.g. $\boldsymbol{v}$ and $\boldsymbol{u}$).
We have defined a vector as an object with both direction and magnitude (length). Let's now consider a pair of vectors with the same direction but different magnitude:
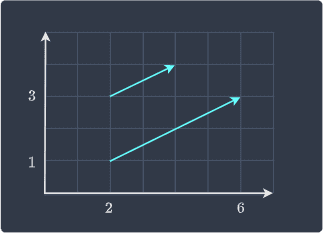
When two vectors are parallel and pointing to the same side like in this case, we say that they have the same direction. The magnitude (length) of the two vectors is different - the bottom vector is twice as long as the top vector.
Next, let's consider the case when two vectors have the same magnitude but different directions:
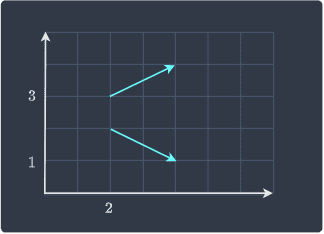
We can see that they have the same length, but they are pointing in two different directions.
Equality of vectors
Two vectors are considered equal if they have the same direction and magnitude.
Consider the vectors $\overrightarrow{AB}$ and $\overrightarrow{CD}$ below:
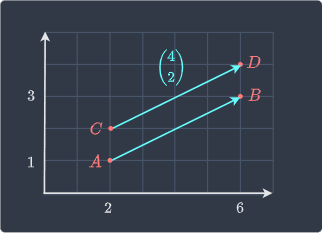
Even though the starting and ending points of the vectors are different, they are considered to be equal because they have the same magnitude (length) and direction. Because we can draw a vector given its magnitude and direction from any point, it is considered to be free. We will later see a non-free vector whose starting point is pinned to the origin (position vector).
Taking scalar multiples of vectors
Scalars are quantities that have a magnitude without any notion of direction. We can multiply a vector by a scalar by multiplying every component of the vector by the scalar. For instance, consider the scalar $c$ and vector $\boldsymbol{v}$ below:
Taking their product gives:
Geometric interpretation of scalar multiples of vectors
Taking a scalar multiple of a vector involves stretching or shrinking the vector and does not change the direction of the vector. For instance, suppose we double the vector $\boldsymbol{a}$ like so:
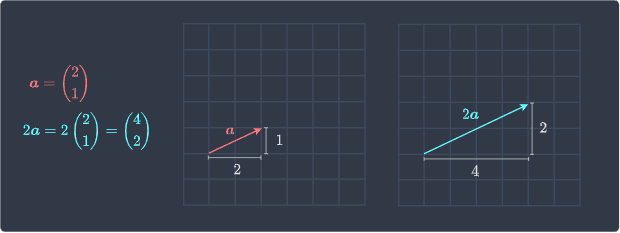
Notice how the length of the new vector $2\boldsymbol{a}$ has doubled, but it is still pointing in the same direction as $\boldsymbol{a}$.
What if we multiply a vector by a negative number? In this case, the new vector will point in the opposite direction, as illustrated below:
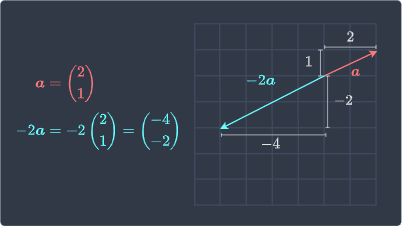
Here, the new vector $-2\boldsymbol{a}$ has doubled in length but is now pointing in the opposite direction because we have multiplied by a negative constant. Note that if we multiply a vector by $-1$, then we only reverse its direction but preserve its length:
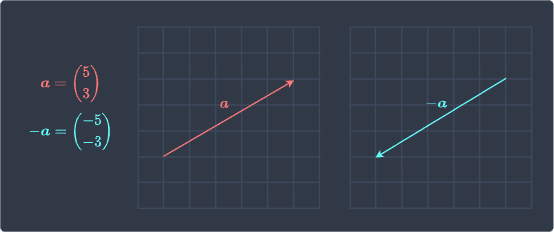
Adding two vectors
Suppose we have the following two vectors:
To add two vectors, we add each pair component-wise:
Vector addition is said to be commutative, which means that the order of the addition does not matter:
Geometric interpretation of vector-vector addition (head-to-tail method)
Consider the same set of vectors $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$ as above:
We know that their sum is:
Geometrically, $\boldsymbol{v}_1+\boldsymbol{v}_2$ represents the green vector below:
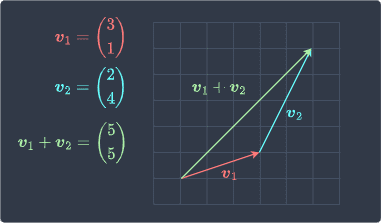
To geometrically add two vectors, we use the so-called head-to-tail method:
we place the tail (non-pointy part) of the second vector ($\color{blue}{\boldsymbol{v}_2}$) at the head of the first vector ($\color{red}{\boldsymbol{v}_1}$).
the vector ${\color{red}{\boldsymbol{v}_1}}+ \color{blue}{\boldsymbol{v}_2}$ is the vector whose tail is at the tail of $\color{red}{\boldsymbol{v}_1}$ and whose head is at the head of the $\color{blue}{\boldsymbol{v}_2}$.
Intuition. The reason why the head-to-tail method works can be explained using the following diagram:
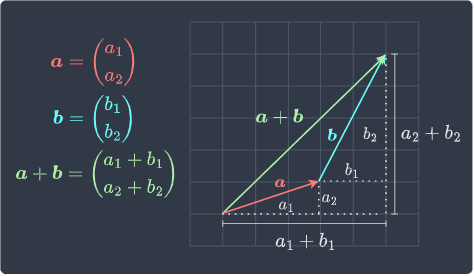
Here, vectors $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$ are denoted as $\boldsymbol{a}$ and $\boldsymbol{b}$ for brevity. We can see that:
the horizontal component for $\boldsymbol{a}+\boldsymbol{b}$ is $a_1+b_1$.
the vertical component for $\boldsymbol{a}+\boldsymbol{b}$ is $a_2+b_2$.
We can also geometrically show that vector addition is commutative:
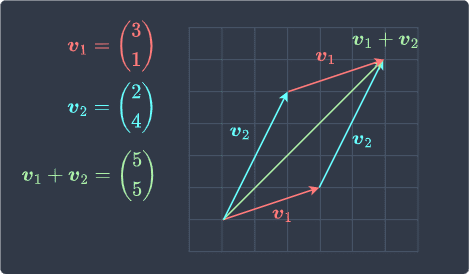
We can see that reversing the order of the addition does not matter - we end up with the green vector either way!
Subtracting two vectors
Consider the following vectors:
Let's now derive vector subtraction using vector addition:
The key trick in deriving vector subtraction is to convert the operation into addition by multiplying the second vector by $-1$.
We already know how to geometrically add two vectors using the head-to-tail method. The same logic applies to subtraction except that we reverse the direction of the second vector since we are multiplying it by $-1$. Here's the diagram:
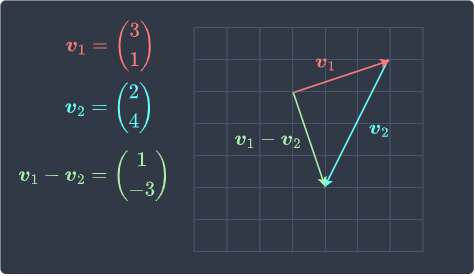
Notice how the direction of $\boldsymbol{v}_2$ is reversed here.
Magnitude of vector
The magnitude of a vector is simply its length.
Computing the magnitude of a vector
For vectors in two-dimensional space, we can use the Pythagoras theorem to determine the magnitude. For instance, consider the following vector:
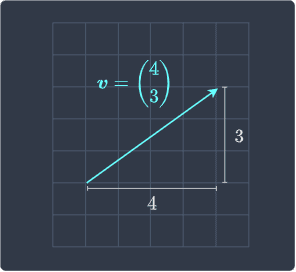
From Pythagoras theorem, we know that the length of $\boldsymbol{v}$, denoted as $\Vert{\boldsymbol{v}}\Vert$ is:
Therefore, the magnitude of $\boldsymbol{v}$ is 5.
Useful property of the magnitude of a vector
If $c$ is a scalar and $\boldsymbol{v}$ is a vector, then:
Where $\vert{c}\vert$ is the absolute value of $c$.
Proof. We will prove the case for vectors in two-dimensional space but the proof can be easily generalized to higher dimensions. Let vector $\boldsymbol{v}$ be denoted as follows:
The scalar-vector product $c\boldsymbol{v}$ is:
Taking the magnitude:
This completes the proof.
Zero vector
A zero vector, which is denoted as $\boldsymbol{0}$, has all zeros as it entries. For instance, the zero vector in two-dimensional space is:
The zero vector has a magnitude of $0$.
Unit vectors
A unit vector is a vector with magnitude one. Typically, unit vectors are denoted by $\boldsymbol{u}$.
Converting vectors into unit vectors
We can convert any vector $\boldsymbol{v}$ (except the zero vector) into a unit vector $\boldsymbol{u}$ while preserving its direction by using the following formula:
Where $\Vert{\boldsymbol{v}}\Vert$ is the magnitude of $\boldsymbol{v}$.
Proof. Let's first prove that $\boldsymbol{u}$ as computed by \eqref{eq:G6SKsOpSuQVO82XzN2F} has a magnitude of one. We have previously proven the following property of the magnitude of a vector:
Where $c$ is any constant and $\vert{c}\vert$ is the absolute value of $c$. We let $c$ be defined as follows:
Substituting this into \eqref{eq:HOTfsE5kD7uSQLKQSeN} gives:
For the second step, we discarded the absolute value because $\Vert{\boldsymbol{v}}\Vert$ is a measure of length and is therefore always positive. The left-hand side of \eqref{eq:L145f21PtXgsMwlPBir} is simply $\Vert{\boldsymbol{u}}\Vert$. Therefore, we conclude that:
Great, we've managed to prove that the vector computed by \eqref{eq:G6SKsOpSuQVO82XzN2F} is a unit vector!
Next, let's prove that $\boldsymbol{u}$ has the same direction as $\boldsymbol{v}$. The relationship between $\boldsymbol{u}$ and $\boldsymbol{v}$ is as follows:
Since the fraction is a scalar value, $\boldsymbol{u}$ is a scalar multiple of $\boldsymbol{v}$. We know from earlierlink that scalar multiples of vector preserve the direction. This completes the proof.
Converting a vector into a unit vector
Consider the following vector:

Convert this vector into a unit vector.
Solution. Firstly, let's compute the magnitude of the vector:
Clearly $\boldsymbol{v}$ is not a unit vector. We can convert $\boldsymbol{v}$ into a unit vector $\boldsymbol{u}$ like so:
Let's confirm that $\boldsymbol{u}$ has a length of one:
Visually, $\boldsymbol{u}$ looks like the following:
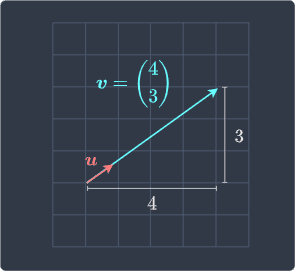
Notice how $\boldsymbol{u}$ preserves the direction of $\boldsymbol{v}$.
Vectors in higher dimensions
Up to now, we have only dealt with vectors in two dimensions. Vectors can exist in higher dimensions as well - for instance, here is a vector in three-dimensional space:
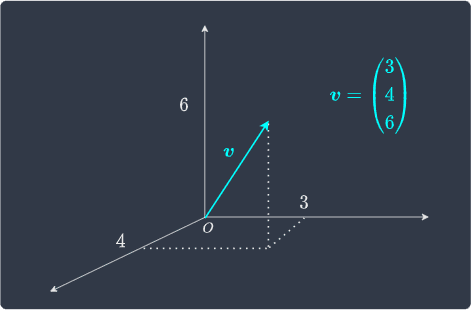
Regardless of what dimension a vector is in, we can always think of it as an arrow that connects one point to another.
Using set notation to describe the dimension of vectors
To denote a vector $\boldsymbol{v}$ in $n$-dimensional space, we use the following set notation:
For instance, a three-dimensional vector is denoted as:
The $\in$ symbol is read as "belongs to".
Practice problems
Compute the following:
Multiply each component by the scalar constant like so:
Compute the following:
To add two vectors, add each pair of components like so:
Compute the following:
To subtract two vectors, perform the subtraction for each pair of components like so:
Consider the following vector:
Compute the magnitude of $\boldsymbol{v}$.
The magnitude represents the length of $\boldsymbol{v}$. We can therefore use the Pythagoras theorem to get:
Consider the following vector:
Convert $\boldsymbol{v}$ into a unit vector.
We first compute the magnitude of the vector:
We then use formula for unit vector:







