Before we dive into the Gram-Schmidt process, let's go through a quick example that demonstrates how we can construct an orthogonal basis given any two basis vectors for $\mathbb{R}^2$.

Solution. Let's start by visualizing the two vectors:

We can clearly see that the two vectors are not perpendicular to each other, which means that they do not form an orthogonal basis for $\mathbb{R}^2$. We can fix one vector, say $\boldsymbol{x}_1$, and modify the other vector $\boldsymbol{x}_2$ such that $\boldsymbol{x}_2$ becomes perpendicular to $\boldsymbol{x}_1$.

Let's set $\boldsymbol{v}_1=\boldsymbol{x}_1$ and our goal is to find $\boldsymbol{v}_2$ where $\boldsymbol{v}_2$ is orthogonal to $\boldsymbol{v}_1$. Recall that $\boldsymbol{v}_2$ can be constructed by projecting $\boldsymbol{x}_2$ onto $\boldsymbol{v}_1$ as shown below:

From the geometric interpretationlink of vector addition, we have the following relationship:

From theorem, we know that:

Substituting \eqref{eq:WnFx9a9ZbZWJGQEa9UF} into \eqref{eq:PsFQHOCQvWAd02tK9IA} gives:

From our diagram, this looks to be correct! Therefore, an orthogonal basis for $\mathbb{R}^2$ is:

The Gram-Schmidt process is a generalization of what we just performed to higher dimensions. To derive the Gram-Schmidt process, we require the following theorem.

Proof. Let $W$ be a finite-dimensional subspace of a vector space $V$ and let $\{\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_r\}$ be an orthogonal basis for $W$. From theoremlink, we know that any vector $\boldsymbol{v}\in{V}$ can be expressed as a sum of two vectors that are orthogonal to each other, that is, $\boldsymbol{v}=\boldsymbol{w}_1+\boldsymbol{w}_2$ where $\boldsymbol{w}_1\in{W}$ and $\boldsymbol{w}_2\in{W}^\perp$. Let $\boldsymbol{w}_1=\mathrm{Proj}_W(\boldsymbol{v})$. By theoremlink, $\boldsymbol{w}_1$ can be expressed as:

Since $\boldsymbol{w}_2$ is orthogonal to the subspace $W$, we have that $\boldsymbol{w}_2$ is orthogonal to every vector of $W$, including the basis vectors $\{\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_r\}$ of $W$. By theoremlink, the dot product of two perpendicular vectors is zero:

Let's modify \eqref{eq:htY2XMEdsQyceWOhHP7} like so:

Now, because $\boldsymbol{v}=\boldsymbol{w}_1+\boldsymbol{w}_2$, this reduces to:

Note that if $\{\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_n\}$ is an orthonormal basis, then the length of each basis vector is one. Therefore, \eqref{eq:PCh2udaAc6cnzmwjYVC} reduces to:

This completes the proof.

Proof. Let $W$ be any subspace for a vector space $V$. Let the basis for $W$ be $\{\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_r\}$.

We first let $\boldsymbol{v}_1=\boldsymbol{w}_1$. Let $W_1$ be the subspace spanned by $\boldsymbol{w}_1$, which means that $\{\boldsymbol{w}_1\}$ is the basis for $W_1$. Since $W_1$ is spanned by a single basis vector, $W_1$ is simply a line. We can construct $\boldsymbol{v}_2$ that is orthogonal to $\boldsymbol{v}_1$ using $\boldsymbol{w}_2$ like so:

Visually, the relationship between the vectors is:

By theoremlink, we can express the projection as:

Substituting \eqref{eq:NOHA67ECOblfxSXhX0m} into \eqref{eq:DlntcNN5PCsJKfkc7Sz} gives:

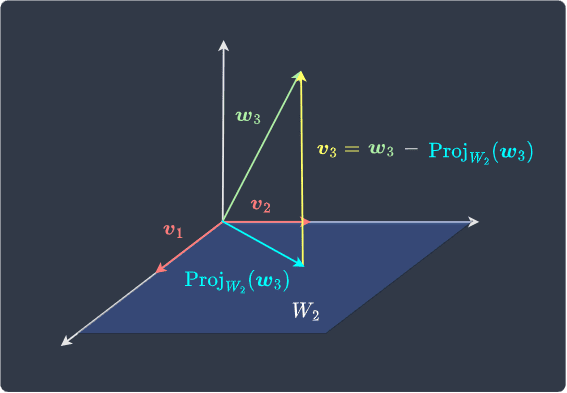
Great, we've managed to find $\boldsymbol{v}_2$ that is orthogonal to $\boldsymbol{v}_1$. Next, to construct $\boldsymbol{v}_3$ that is orthogonal to both $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$ using $\boldsymbol{w}_3$, we find a vector orthogonal to the subspace $W_2$ spanned by $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$. Since $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$ are linearly independent and span $W_2$, they form a basis for $W_2$. Note that, unlike $W_1$ which traced a line, $W_2$ is a flat plane.

Now, $\boldsymbol{v}_3$ can be computed by:

Visually, the relationship between the vectors is:

By theoremlink, because $\{\boldsymbol{v}_1,\boldsymbol{v}_2\}$ is a basis for $W_2$, we know that $\mathrm{Proj}_{W_2}(\boldsymbol{w}_3)\in{W_2}$ can be written as:

Therefore, \eqref{eq:C263WvfQPmXAvC5J3zj} becomes:

We've now managed to find three vectors $\boldsymbol{v}_1$, $\boldsymbol{v}_2$ and $\boldsymbol{v}_3$ that are orthogonal! Now, $\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\}$ form a basis for the subspace $W_3$. Similarly, to construct $\boldsymbol{v}_4$ that is orthogonal to these vectors using $\boldsymbol{w}_4$, we compute:

We keep on repeating this process until we end up with an orthogonal basis for $W$. Remember, if $W$ originally had $r$ basis vectors, then we must continue this process until we get $r$ orthogonal basis vectors. This completes the proof.

Solution. Let $\boldsymbol{v}_1=\boldsymbol{w}_1$. Next, $\boldsymbol{v}_2$, which is orthogonal to $\boldsymbol{v}_1$, can be constructed by:

Finally, $\boldsymbol{v}_3$, which is orthogonal to both $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$, can be constructed by:

By the Gram-Schmidt process, we have managed to construct an orthogonal basis $\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\}$ for $\mathbb{R}^3$ where:

Let's still confirm that $\boldsymbol{v}_1$, $\boldsymbol{v}_2$ and $\boldsymbol{v}_3$ are orthogonal:

Indeed, $\{\boldsymbol{v}_1,\boldsymbol{v}_2,\boldsymbol{v}_3\}$ is an orthogonal basis for $\mathbb{R}^3$.

There are two ways to obtain an orthonormal basis using the Gram-Schmidt process:

• in the end, convert each orthogonal basis vector into a unit vector by theoremlink.

• at every step, convert the constructed orthogonal basis vector into a unit vector.

If we take the latter approach, the Gram-Schmidt process can be expressed as below.

Proof. Recall the Gram-Schmidt process used for constructing an orthogonal basis:

Where $\{\boldsymbol{v}_1,\boldsymbol{v}_2,\cdots,\boldsymbol{v}_r\}$ is an orthogonal basis. At step $1$, we can convert $\boldsymbol{v}_1$ into a unit vector $\boldsymbol{q}_1$ by using theoremlink. Because $\Vert\boldsymbol{q}_1\Vert=1$, step $2$ can now be simplified to:

We now convert $\boldsymbol{v}_2$ into a unit vector $\boldsymbol{q}_2$, which gives us an orthonormal set $\{\boldsymbol{q}_1, \boldsymbol{q}_2\}$. Step $3$ can be written as:

For step $r$, we have the following

Note that to obtain a complete orthonormal basis, we will have to convert $\boldsymbol{v}_r$ into a unit vector as well. This completes the proof.

Proof. Suppose we use the variantlink of the Gram-Schmidt process in which we build up an orthonormal basis at every step. The $i$-th orthogonal basis vector is constructed by:

Multiplying both sides by $\frac{1}{\Vert\boldsymbol{v}_i\Vert}$ gives:

The left-hand side is equal to the unit vector $\boldsymbol{q}_i$ by definitionlink and so:

Now, performing a dot product with $\boldsymbol{q}_i$ on both sides gives:

This completes the proof.

Proof. Recall that we start the Gram-Schmidt process by setting $\boldsymbol{v}_1=\boldsymbol{w}_1$. We then select $\boldsymbol{v}_2$ such that $\boldsymbol{v}_2$ is orthogonal to the subspace $W_1$ spanned by $\boldsymbol{v}_1$. Since $\boldsymbol{w}_1\in{W}_1$, we have that:

In the 2nd step, we select $\boldsymbol{v}_3$ such that $\boldsymbol{v}_3$ is orthogonal to the subspace $W_2$ spanned by $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$. Recall the relationship between $\boldsymbol{w}_2$ and $\boldsymbol{v}_2$ below:

Where $\mathrm{Proj}_{W_1}(\boldsymbol{w}_2)\in{W_1}$. Because $W_1$ is spanned by $\boldsymbol{v}_1$, we know that $\mathrm{Proj}_{W_1}(\boldsymbol{w}_2)$ can be expressed as some linear combination of $\boldsymbol{v}_1$. This means that $\boldsymbol{w}_2$ can be expressed as some linear combination of $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$. Because $W_2$ is spanned by $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$, we have that $\boldsymbol{w}_2\in{W_2}$. Also $\boldsymbol{w}_1\in{W_2}$ since $\boldsymbol{w}_1\in{W_1}$ where $W_1$ is spanned by $\boldsymbol{v}_1$. Because $\boldsymbol{w}_1,\boldsymbol{w}_2\in{W_2}$ and $\boldsymbol{v}_3$ is orthogonal to any vector in $W_2$, we have that:

In the 3rd step, we select $\boldsymbol{v}_4$ such that $\boldsymbol{v}_4$ is orthogonal to the subspace $W_3$ spanned by $\boldsymbol{v}_1$, $\boldsymbol{v}_2$ and $\boldsymbol{v}_3$. Recall the relationship between $\boldsymbol{v}_3$ and $\boldsymbol{w}_3$ below:

Where $\mathrm{Proj}_{W_2}(\boldsymbol{w}_3)\in{W_2}$. This means that $\boldsymbol{w}_3$ can be expressed as some linear combination of $\boldsymbol{v}_3$ and the basis vectors of $W_2$, which we know are $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$. Because $W_3$ is spanned by $\boldsymbol{v}_1$, $\boldsymbol{v}_2$ and $\boldsymbol{v}_3$, we have that $\boldsymbol{w}_3\in{W_3}$. Next, we already established that:

• $\boldsymbol{w}_2\in{W}_2$ where $W_2$ is spanned by $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$.

• $\boldsymbol{w}_1\in{W}_1$ where $W_1$ is spanned by $\boldsymbol{v}_1$.

Therefore, we have that $\boldsymbol{w}_1,\boldsymbol{w}_2,\boldsymbol{w}_3\in{W_3}$. The vector $\boldsymbol{v}_4$ is orthogonal to any vector in $W_3$, which means that:

In general, in the $j$-th step, we add a vector $\boldsymbol{v}_{j+1}$ into the list of orthogonal vectors of $\boldsymbol{w}_1$, $\boldsymbol{w}_2$, $\cdots$, $\boldsymbol{w}_{j}$. In other words, $\boldsymbol{w}_i$ is orthogonal to $\boldsymbol{v}_{i+1}$ for $i=1,2,\cdots,n-1$. This completes the proof.