What is dot product? When we are dealing with real numbers, there is only one interpretation of product - multiplication. However, in the world of vectors, there are two types of products - dot product and cross product . The dot product appears everywhere in machine learning and is therefore a must-know topic. In this guide, we will explore the dot product in depth!
Definition.
Dot product
Suppose we have the following two vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ :
$$\boldsymbol{v}=\begin{pmatrix}
v_1\\
v_2\\
v_3\\
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=\begin{pmatrix}
w_1\\
w_2\\
w_3\\
\end{pmatrix}$$
The dot product is defined as:
$$\boldsymbol{v}\cdot{\boldsymbol{w}}=
v_1w_1+
v_2w_2+
v_3w_3$$
Note that $\boldsymbol{v}$ and $\boldsymbol{w}$ are in $\mathbb{R}^3$ , but the dot product returns a scalar. The dot product is also sometimes referred to as the scalar product or the inner product .
Example.
Computing the dot product between two vectors
Compute the dot product $\boldsymbol{v}\cdot{\boldsymbol{w}}$ where $\boldsymbol{v}$ and $\boldsymbol{w}$ are defined as:
$$\boldsymbol{v}=
\begin{pmatrix}
1\\2
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=
\begin{pmatrix}
3\\4
\end{pmatrix}$$
Solution . The dot product $\boldsymbol{v}\cdot\boldsymbol{w}$ is:
$$\begin{align*}
\boldsymbol{v}\cdot{\boldsymbol{w}}&=
(1)(3)+(2)(4)\\
&=11
\end{align*}$$
Theorem.
Using dot product to compute the angle between two vectors
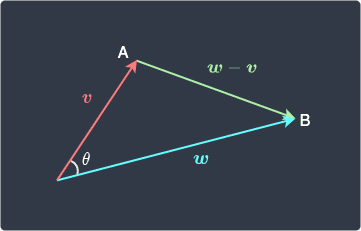
Suppose we have the following two vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ :
Let the angle between $\boldsymbol{v}$ and $\boldsymbol{w}$ be $\theta$ . The dot product of $\boldsymbol{v}$ and $\boldsymbol{w}$ is:
$$\boldsymbol{v}\cdot{\boldsymbol{w}}=
\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert
\cos{(\theta)}$$
Here, $ \Vert{\boldsymbol{v}}\Vert$ is the magnitude of $\boldsymbol{v}$ . We can also rearrange this to get:
$$\cos{(\theta)}=
\frac{\boldsymbol{v}\cdot{\boldsymbol{w}}}
{\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert}$$
Proof . Suppose we have the following:
Here, the vector $\boldsymbol{w}-\boldsymbol{v}$ points from $A$ to $B$ because of the geometric interpretation of vector addition link
The lengths of the sides are:
Using the cosine rule from elementary trigonometry, we have that:
$$\begin{equation}\label{eq:xF6GwOYW3PvcsraNGkP}
\Vert{\boldsymbol{w}-\boldsymbol{v}}\Vert^2
=\Vert\boldsymbol{v}\Vert^2+
\Vert\boldsymbol{w}\Vert^2-2\Vert{\boldsymbol{v}}\Vert
\Vert{\boldsymbol{w}}\Vert\cos(\theta)
\end{equation}$$
Let's assume $\boldsymbol{w}$ and $\boldsymbol{v}$ are both in $\mathbb{R}^3$ , though the proof can easily be generalized to $\mathbb{R}^n$ . The vector $\boldsymbol{w}-\boldsymbol{v}$ is:
$$\boldsymbol{w}-\boldsymbol{v}
=\begin{pmatrix}
w_1-v_1\\
w_2-v_2\\
w_3-v_3\\
\end{pmatrix}$$
The square of the magnitude of $\boldsymbol{w}-\boldsymbol{v}$ is:
$$\begin{align*}
\Vert{\boldsymbol{w}-\boldsymbol{v}}\Vert^2
&=
\Big(\;\sqrt{(w_1-v_1)^2+
(w_2-v_2)^2+
(w_3-v_3)^2}\;\Big)^2\\
&=
(w_1-v_1)^2+
(w_2-v_2)^2+
(w_3-v_3)^2
\end{align*}$$
Similarly, $\Vert{\boldsymbol{v}}\Vert^2$ and $\Vert{\boldsymbol{w}}\Vert^2$ are:
$$\begin{align*}
\Vert{\boldsymbol{v}}\Vert^2
&=
v_1^2+v^2_2+v^3_3\\
\Vert{\boldsymbol{w}}\Vert^2
&=
w_1^2+w^2_2+w^3_3
\end{align*}$$
Substituting these squared magnitudes into \eqref{eq:xF6GwOYW3PvcsraNGkP} gives:
$$\begin{align*}
(w_1-v_1)^2+
(w_2-v_2)^2+
(w_3-v_3)^2&=
v^2_1+v^2_2+v^2_3+
w^2_1+w^2_2+w^2_3
-2
\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert\cos{(\theta)}
\\
v_1w_1+v_2w_2+v_3w_3&=\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert\cos{(\theta)}\\
\boldsymbol{v}\cdot{\boldsymbol{w}}&=\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert\cos{(\theta)}
\end{align*}$$
This completes the proof.
Example.
Computing the angle between two vectors
Compute the angle between the following two vectors:
$$\boldsymbol{v}=
\begin{pmatrix}
2\\
3
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=
\begin{pmatrix}
4\\
1
\end{pmatrix}$$
Solution . We know from theorem link
$$\boldsymbol{v}\cdot{\boldsymbol{w}}=
\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert
\cos{(\theta)}$$
Rearranging the above to make $\theta$ the subject:
$$\begin{align*}
\theta&=
\arccos{\Big(\frac{\boldsymbol{v}\cdot{\boldsymbol{w}}}
{\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert}\Big)}\\
&=\mathrm{arccos}{\Big(\frac{(2)(4)+(3)(1)}
{(2^2+3^2)^{1/2}(4^2+1^2)^{1/2}}\Big)}\\
&\approx42.5
\end{align*}$$
Therefore, the angle between vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ is around $42.5$ degrees. This is confirmed visually below:
Properties of dot products
Theorem.
Dot product of two perpendicular vectors
If $\boldsymbol{v}$ and $\boldsymbol{w}$ are vectors that are perpendicular to each other, then:
$$\boldsymbol{v}\cdot{\boldsymbol{w}}=0$$
Proof . If $\boldsymbol{v}$ and $\boldsymbol{w}$ are perpendicular, then we have the following scenario:
From theorem link
$$\begin{align*}
\boldsymbol{v}\cdot{\boldsymbol{w}}&=
\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert
\cos{(\theta)}\\
&=
\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert
\cos{(90)}\\
&=
0
\end{align*}$$
This completes the proof.
Theorem.
Commutative property of dot product
The commutative property of the dot product states that the ordering of the dot product between two vectors does not matter:
$$\boldsymbol{v}\cdot\boldsymbol{w}=
\boldsymbol{w}\cdot\boldsymbol{v}$$
Proof . We will prove the case for $\mathbb{R}^3$ here, but the proof can easily be generalized for $\mathbb{R}^n$ . Let vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ be:
$$\boldsymbol{v}=
\begin{pmatrix}
v_1\\v_2\\v_3\\
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=
\begin{pmatrix}
w_1\\w_2\\w_3\\
\end{pmatrix}$$
Starting from the left-hand side:
$$\begin{align*}
\boldsymbol{v}\cdot\boldsymbol{w}&=
v_1w_1+v_2w_2+v_3w_3\\
&=w_1v_1+w_2v_2+w_3v_3\\
&=\boldsymbol{w}\cdot\boldsymbol{v}
\end{align*}$$
This completes the proof.
Theorem.
Position of scalars can be changed
If $\boldsymbol{a}$ and $\boldsymbol{b}$ are vectors in $\mathbb{R}^n$ and $\lambda$ is some constant scalar, then:
$$(\lambda{\boldsymbol{v}})\cdot{\boldsymbol{w}}=
\boldsymbol{v}\cdot(\lambda{\boldsymbol{w}})
=\lambda(\boldsymbol{v}\cdot\boldsymbol{w})$$
Proof . We will prove the case for $\mathbb{R}^3$ here, but the proof can easily be generalized for $\mathbb{R}^n$ . Let vectors $\boldsymbol{v}$ and $\boldsymbol{w}$ be:
$$\boldsymbol{v}=
\begin{pmatrix}
v_1\\v_2\\v_3\\
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=
\begin{pmatrix}
w_1\\w_2\\w_3\\
\end{pmatrix}$$
Starting from the left-hand side:
$$\begin{align*}
(\lambda\boldsymbol{v})\cdot{\boldsymbol{w}}&=
\begin{pmatrix}
\lambda{v_1}\\\lambda{v_2}\\\lambda{v_3}\\
\end{pmatrix}\cdot
\begin{pmatrix}
w_1\\w_2\\w_3\\
\end{pmatrix}\\
&=\lambda{v_1w_1}+\lambda{v_2w_2}+\lambda{v_3w_3}
\end{align*}$$
To prove the first equality:
$$\begin{align*}
(\lambda\boldsymbol{v})\cdot{\boldsymbol{w}}
&=\lambda{v_1w_1}+\lambda{v_2w_2}+\lambda{v_3w_3}\\
&=v_1(\lambda{w_1})+v_2(\lambda{w_2})+v_3(\lambda{w_3})\\
&=\boldsymbol{v}\cdot(\lambda{\boldsymbol{w}})
\end{align*}$$
To prove the second equality:
$$\begin{align*}
(\lambda\boldsymbol{v})\cdot{\boldsymbol{w}}
&=\lambda{v_1w_1}+\lambda{v_2w_2}+\lambda{v_3w_3}\\
&=\lambda(v_1w_1)+\lambda(v_2w_2)+\lambda(v_3w_3)\\
&=\lambda(\boldsymbol{v}\cdot\boldsymbol{w})
\end{align*}$$
This completes the proof.
Theorem.
Dot Product Distributes Over Vector Addition
If $\boldsymbol{u}$ , $\boldsymbol{v}$ and $\boldsymbol{w}$ are vectors in $\mathbb{R}^n$ , then:
$$\begin{align*}
(\boldsymbol{u}+\boldsymbol{v})\cdot\boldsymbol{w}=
\boldsymbol{u}\cdot\boldsymbol{w}+\boldsymbol{v}\cdot\boldsymbol{w}
\end{align*}$$
Proof . We will prove the case for $\mathbb{R}^3$ here, but the proof can easily be generalized for $\mathbb{R}^n$ . Let vectors $\boldsymbol{u}$ , $\boldsymbol{v}$ and $\boldsymbol{w}$ be as follows:
$$\boldsymbol{u}=
\begin{pmatrix}
u_1\\u_2\\u_3\\
\end{pmatrix},\;\;\;\;
\boldsymbol{v}=
\begin{pmatrix}
v_1\\v_2\\v_3\\
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=
\begin{pmatrix}
w_1\\w_2\\w_3\\
\end{pmatrix}$$
The vector $\boldsymbol{u}+\boldsymbol{v}$ is:
$$\boldsymbol{u}+\boldsymbol{v}=
\begin{pmatrix}
u_1+v_1\\u_2+v_2\\u_3+v_3\\
\end{pmatrix}$$
The left-hand side $(\boldsymbol{u}+\boldsymbol{v})\cdot\boldsymbol{w}$ is therefore:
$$\begin{align*}
(\boldsymbol{u}+\boldsymbol{v})\cdot\boldsymbol{w}&=
\begin{pmatrix}
u_1+v_1\\u_2+v_2\\u_3+v_3\\
\end{pmatrix}\cdot
\begin{pmatrix}
w_1\\w_2\\w_3
\end{pmatrix}\\&=
w_1u_1+w_1v_1+
w_2u_2+w_2v_2+
w_3u_3+w_3v_3
\\&=(w_1u_1+w_2u_2+w_3u_3)+(w_1v_1+w_2v_2+w_3v_3)
\\&=\boldsymbol{u}\cdot{\boldsymbol{w}}+\boldsymbol{v}\cdot\boldsymbol{w}
\end{align*}$$
This completes the proof.
Relationship between magnitude and dot product The following relationships between vector magnitude and dot product is useful for future proofs.
Theorem.
Dot product of a vector with itself is equal to the square of the vector's magnitude
The magnitude of a vector $\boldsymbol{v}$ can be expressed as dot product like so:
$$\Vert{\boldsymbol{v}}\Vert
=(\boldsymbol{v}\cdot\boldsymbol{v})^{1/2}$$
Taking the square on both sides gives:
$$\Vert{\boldsymbol{v}}\Vert^2
=\boldsymbol{v}\cdot\boldsymbol{v}$$
Proof . Consider the following vector:
$$\boldsymbol{v}=\begin{pmatrix}
v_1\\
v_2\\
\vdots\\
v_n\\
\end{pmatrix}$$
By definition, the magnitude of $\boldsymbol{v}$ is:
$$\begin{align*}
\Vert\boldsymbol{v}\Vert
&=(v_1^2+v_2^2+\cdots+v_n^2)^{1/2}\\
&=\Big((v_1)(v_1)+(v_2)(v_2)+\cdots+(v_n)(v_n)\Big)^{1/2}\\
&=(\boldsymbol{v}\cdot\boldsymbol{v})^{(1/2)}
\end{align*}$$
This completes the proof.
Theorem.
Expressing dot product of two vectors using magnitude (2)
If $\boldsymbol{v}$ and $\boldsymbol{w}$ are vectors, then:
$$\boldsymbol{v}\cdot{\boldsymbol{w}}=
\frac{1}{4}\Vert\boldsymbol{v}+\boldsymbol{w}\Vert^2-
\frac{1}{4}\Vert\boldsymbol{v}-\boldsymbol{w}\Vert^2$$
Proof . Let's start from the right-hand side:
$$\begin{align*}
\Vert\boldsymbol{v}+\boldsymbol{w}\Vert^2&=
(\boldsymbol{v}+\boldsymbol{w})\cdot(\boldsymbol{v}+\boldsymbol{w})\\
&=
(\boldsymbol{v}\cdot\boldsymbol{v})+
2(\boldsymbol{v}\cdot\boldsymbol{w})+(\boldsymbol{w}\cdot\boldsymbol{w})\\
&=
\Vert\boldsymbol{v}\Vert^2+
2(\boldsymbol{v}\cdot\boldsymbol{w})+
\Vert\boldsymbol{w}\Vert^2\\
\end{align*}$$
Note that the first step follows from theorem link
Similarly, we have that:
$$\begin{align*}
\Vert\boldsymbol{v}-\boldsymbol{w}\Vert^2&=
(\boldsymbol{v}-\boldsymbol{w})\cdot(\boldsymbol{v}-\boldsymbol{w})\\
&=
(\boldsymbol{v}\cdot\boldsymbol{v})-
2(\boldsymbol{v}\cdot\boldsymbol{w})+(\boldsymbol{w}\cdot\boldsymbol{w})\\
&=
\Vert\boldsymbol{v}\Vert^2-
2(\boldsymbol{v}\cdot\boldsymbol{w})+
\Vert\boldsymbol{w}\Vert^2\\
\end{align*}$$
Therefore:
$$\begin{align*}
\frac{1}{4}\Vert\boldsymbol{v}+\boldsymbol{w}\Vert^2-
\frac{1}{4}\Vert\boldsymbol{v}-\boldsymbol{w}\Vert^2&=
\frac{1}{4}(
\Vert\boldsymbol{v}\Vert^2+
2(\boldsymbol{v}\cdot\boldsymbol{w})+
\Vert\boldsymbol{w}\Vert^2
)-\frac{1}{4}
(\Vert\boldsymbol{v}\Vert^2-
2(\boldsymbol{v}\cdot\boldsymbol{w})+
\Vert\boldsymbol{w}\Vert^2)\\
&=\frac{1}{2}(\boldsymbol{v}\cdot\boldsymbol{w})+
\frac{1}{2}(\boldsymbol{v}\cdot\boldsymbol{w})\\
&=\boldsymbol{v}\cdot\boldsymbol{w}
\end{align*}$$
This completes the proof.
Practice problems Suppose we have the following vectors:
$$\boldsymbol{v}=
\begin{pmatrix}
3\\2
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=
\begin{pmatrix}
1\\4
\end{pmatrix}$$
Compute their dot product.
Your answer
Submit answer
Show solution
The product of the two vectors is:
$$\begin{align*}
\boldsymbol{v}\cdot
\boldsymbol{w}&=
\begin{pmatrix}3\\2\end{pmatrix}\cdot
\begin{pmatrix}1\\4\end{pmatrix}\\
&=(3)(1)+(2)(4)\\
&=11\\
\end{align*}$$
Consider the following two vectors:
$$\boldsymbol{v}=
\begin{pmatrix}
1\\3
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=
\begin{pmatrix}
3\\4
\end{pmatrix}$$
Find the angle (rounded to 1st decimal place) between the two vectors.
Your answer
Submit answer
Show solution
We use theorem link
$$\cos{(\theta)}=
\frac{\boldsymbol{v}\cdot{\boldsymbol{w}}}
{\Vert{\boldsymbol{v}}\Vert\Vert{\boldsymbol{w}}\Vert}$$
Where $\Vert{\boldsymbol{v}}\Vert$ and $\Vert{\boldsymbol{w}}\Vert$ are the magnitude of $\boldsymbol{v}$ and $\boldsymbol{w}$ respectively, while $\theta$ is the angle we are after.
The numerator is:
$$\begin{align*}
\boldsymbol{v}\cdot\boldsymbol{w}
&=(1)(3)+(3)(4)\\
&=15
\end{align*}$$
The denominator is:
$$\begin{align*}
\Vert\boldsymbol{v}\Vert\Vert\boldsymbol{w}\Vert&=
\left(\sqrt{1^2+3^2}\right)
\left(\sqrt{3^2+4^2}\right)\\
&=5\sqrt{10}
\end{align*}$$
The angle $\theta$ is:
$$\cos(\theta)=\frac{15}{5\sqrt{10}}\approx18.4^\circ$$
Consider the following vectors:
$$\boldsymbol{v}=
\begin{pmatrix}
4\\2
\end{pmatrix},\;\;\;\;
\boldsymbol{w}=
\begin{pmatrix}
-1\\2
\end{pmatrix}$$
Show that the two vectors are perpendicular.
To show that these vectors are perpendicular, we can use theorem link
$$\begin{align*}
\boldsymbol{v}\cdot\boldsymbol{w}&=
(4)(-1)+(2)(2)\\&=
0
\end{align*}$$
Since their dot product is zero, $\boldsymbol{v}$ and $\boldsymbol{w}$ must be perpendicular.
Consider the following vector:
$$\boldsymbol{v}=\begin{pmatrix}5\\3\end{pmatrix}$$
Use dot product to compute the square of its magnitude, that is, $\Vert{\boldsymbol{v}}\Vert^2$ .
Your answer
Submit answer
Show solution
By theorem link
$$\begin{align*}
\Vert{\boldsymbol{v}}\Vert^2&=
\boldsymbol{v}\cdot\boldsymbol{v}\\
&=5^2+3^2\\
&=34
\end{align*}$$