
Performing linear regression in NumPy
Start your free 7-days trial now!
Linear regression, in essence, is about computing the line of best fit given some data points. We can use NumPy's polyfit(~) method to find this line of best fit easily.
Here's some toy dataset, which we will visualize using matplotlib:
import matplotlib.pyplot as plt
x = [1,2,4,5]y = [1,4,5,6]plt.scatter(x, y)plt.show()
This produces the following:
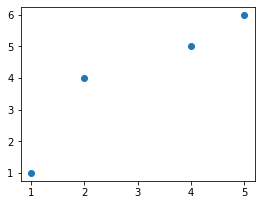
Our goal is to fit a linear line through the data points. We do this by using Numpy's polyfit(~) method:
fitted_coeff = np.polyfit(x, y, deg=1)print(fitted_coeff)
array([1.1, 0.7])
Here, the deg=1 just means that we want to fit a degree 1 polynomial, that is, the line y=mx+b. The returned values are the coefficients of the line of best fit, and the first value is the coefficient of the largest degree, that is, m=1.1 and b=0.7.
Let's graph the line of best fit to see how good it is:
x = [1,2,4,5]y = [1,4,5,6]plt.scatter(x, y)
line_x = np.linspace(1, 5, 100)plt.plot(line_x, line_x * fitted_coeff[0] + fitted_coeff[1])
plt.show()
This produces the following:
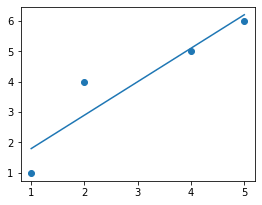
This looks like a solid fit.
Numpy's polyfit(~) method is just for computing the line of best fit
Numpy's polyfit(~) method does not compute any statistical measures like residuals and p-values. This method is only used when you just need the coefficients - nothing more, nothing less.
To perform linear regression at a more comprehensive level, use scipy.stats.linregress.






